Ch6-集合论
集合的概念和表示方式
集合是一些确定的,可以区分的事物汇聚在一起组成的一个整体,组成一个集合的每个事物称为该集合的一个元素,或简称一个元。
定义了 .
集合的表示方式
外延表示法——一一列举出集合的全体元素。
内涵表示法——用谓词表示集合中元素的性质。
可知, 且 .
递归方式定义集合:
集合之间的关系
集合相等:.
集合包含:
集合真包含 .
证明,.
辨析:
. 错
. 对
. 对
. 对
空集和全集
集合的运算
定义,对于集合 :
并集 定义为 .
交集 定义为 .
差集(又称 对 的相对补集).
余集(又称 的绝对补集). 其中 为全集。
对称差 定义为 .
广义交和广义并
规定 ,规定 无意义。
因为任意 , 必然为 F,则不管什么样的 都可以称为 的元素。
用广义交和广义并定义并集和交集:
幂集
幂集一定是一个集合
例如:
幂集的性质:
笛卡尔积
如何表示两个元素的次序?二元有序对 应该具有以下性质:
.
.
有序对 定义为 .
不能写作 .
证明该定义符合有序对的性质:.
左推右显然。右推左:
当 ,则 ,因此,.
当 ,则只能 .
元有序对可以递归定义:
当 ,定义为 .
当 ,定义为 .
Q:能不能这样定义:?
不能分清
笛卡尔积可以定义为:
当 时可以简写为 .
集合运算的优先权
一元运算符
二元运算符()
集合关系符()
一元联结词()
二元联结词()
逻辑关系符()
集合的图形表示
集合运算的关系和证明
集合基本运算的性质
利用定义的证明:证明 . 利用 .
证明 .
利用性质的证明:
证明:对于任意的集合 ,有:
因为:
差集的性质
.
. (可以消去 符号)
.
.
对称差的性质
交换律 .
结合律 .
分配律 .
同一律 .
零律 .
证明 .
对于任意的 ,给出 的充要条件。
即 .
包含关系的性质
. 类比:.
.
.
.
.
.
幂集合的性质
先复习幂集合的定义:
满足性质:
. 证明:
前提.
前提.
. 利用上面的结论:
.
反过来不成立,例如 . 但 ,.
.
先证明,若 ,等价于 且 ,等价于 且 . 等价于 . 等价于 .
其中一步的证明: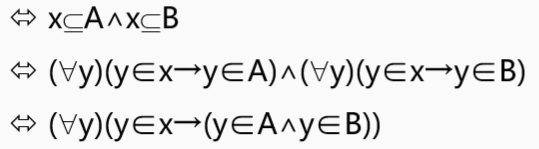
.
因为 . 但是 .
.
若 ,当 不是空集,则 ,可推出 .
因此,. 也就是 .
当 ,则显然成立。
还可以?首先,
.
传递集合
如果集合的集合 的任一元素的元素都是 的元素,就称 为传递集合,这个定义也可以写成:
等价于:
例如, 不是传递集合。
定理:对集合的集合 , 是传递集合 .
先设 是传递集合,则对任意的 ,若 则 . 若 ,则对于 ,有 (因为传递集合的性质),则有 ( 中每个元素都是 的元素),因此 .
上面我们说明了当 是传递集合时,,也就是 .
再设 ,则对于 有:
因此,当 , 是传递集合。
对集合的集合 ,
是传递集合是传递集合 先设 是传递集合,对于任意的 有:
再设 是传递集合,对于任意的 有:
广义并和广义交的性质
对集合的集合 ,有:
.
,其中 非空。
证明:利用广义交和广义并的定义。
.
.
证明第一个:
对于 ,有:
.
对于 ,有:
说明了,广义并是幂集的“逆运算”但是 ,只有 .
若 是传递集合,则 是传递集合。
我们证明 是传递集合,其中运用 是传递集合的条件。
对于任意 ,有:
因为广义并的定义因为是传递集合 若集合 的元素都是传递集合,则 是传递集合。
是传递集合 若非空集合 是传递集合,则 是传递集合,且 .
需要使用正则公理。这里暂时不证明
若非空集合 的元素都是传递集合,则 是传递集合。
因为,是传递集合因为任意
笛卡尔积的性质
笛卡尔积可以定义为:
有序对 定义为 .
.
若 且 且 ,则 .
注意条件,少一个都不能满足。
.
因为 .
.
若 是集合,,则 .()
.
.
由以上两式可以得到:
证明 .
利用结论 4. 我们有:
对于任意集合 ,若 ,则:
利用结论 4. 其实就是对应属于。
对于任意非空集合 ,有:
先设 ,对于任意的 ,存在 ,则:
所以 ,,类似地 .
再设 ,则:
也就证明了 .
集合的基数
集合的基数就是集合中元素的个数。
有限集合的基数
如果存在 ,使得集合 与集合 的元素个数相等,就说集合 的基数是 ,记作 或 或 ,空集的基数是零。
幂集和笛卡尔积的基数
对于有限集合 ,
证明,使用二项式定理。
自然数集的大小和自然数集的幂集一样大吗?
基本运算的基数
.
.
.
.
.
.
证明:将 拆分为 和 ……
容斥原理
若 且 , 是有限集合,则:
集合论公理体系
集合论公理体系是一阶谓词公理系统的扩展,包括一阶谓词公理和几个集合论公理。目的是构造出所有合法的集合,集合论的所有元素都是集合,只研究集合。空集是最基本的集合。
外延公理
空集存在公理
无序对集合存在公理
构造出以两个集合为元素的集合。
并集合公理
对于任意的集合 ,存在一个集合 ,它的元素恰好为 中元素的元素。
也就是广义并。解决了广义并的存在性。
子集公理模式
对于任意的谓词公式 ,对任意的集合 ,存在一个集合 ,它的元素 恰好既是 的元素又能使 为真。
可以解决交集、差集、广义交和笛卡尔积的存在性:
令 ,则对于任意的集合 ,存在一个集合 ,它的元素 既满足 又满足 .
令 ,则可以证明差集的存在性。
令 ,则可以证明广义交的存在性。
先找到一个集合 ,使得 包含所有的 ,前面说明了,可以取 .
因此,可以选取公式 .
选取:
幂集合公理
对于任意的集合 ,存在一个集合 ,它的元素恰好是 的子集。
说明了子集的存在性。
正则公理
对于任意的非空集合 ,存在 的一个元素,它和 不相交。
解决了奇异集合。
无穷公理
存在一个由所有自然数构成的集合:
替换公理模式
对于任意的谓词公式 ,如果对于任意的 存在唯一的 使得 为真(相当于函数单射),则对于所有的集合 ,就存在一个 ,使得 中的元素 恰好是 中元素 所对应的哪些 .
替换公理模式 子集公理模式。
选择公理
关系函数
解决了 Russel 悖论:不存在集合 ,使得任意集合都是 的元素。
如果存在这样的集合,选择 ,则构造:
若取 ,则 ,如果 ,就有 ,矛盾。
为什么规定 不存在。
正则公理和奇异集合 首先定义极小元:对于任意集合 ,当 且 ,则称 是 的一个极小元。正则公理是说一个集合必然存在极小元。
证明:对于任意集合 ,。假设 ,构造 ,则 ,且 存在极小元,只能是 ,则 ,但是 ,矛盾。
证明:对于任意的集合 有:
假设不成立,构造集合 ,则 存在极小元,
证明:对于任意的非空的传递集合 ,有 .
证明:定义奇异集合 ,满足 ,,而且:
根据正则公理,奇异集合不存在,可以取 ,则假设 中有极小元 ,有:
而 ,这会使得:
因此矛盾。
无穷公理和自然数集合
对于任意集合 ,可以定义集合 ,把 称为 的后继。
定义自然数:
也就是对于 ,定义:
对于任意自然数 ,有:
集合的三歧性:对于 的元素 : 中恰好成立一个。
自然数的三歧性:即 中恰好成立一个。