[TOC]
# Ch6-集合论
### 集合的概念和表示方式
集合是一些确定的,可以区分的事物汇聚在一起组成的一个整体,组成一个集合的每个事物称为该集合的一个元素,或简称一个元。
定义了 $a\in A,b \notin A$.
- 集合的元素可以是任何事物,也可以是另外的集合,但是集合中的元素不能是该集合自身。
**集合的表示方式**
- 外延表示法——一一列举出集合的全体元素。
$$
A=\{7,8,9\}, N=\{0,1,2,3,\cdots\}
$$
- 内涵表示法——用谓词表示集合中元素的性质。
$$
A=\{x\mid x 是整数\},B=\{y\mid P(y)\}
$$
可知,$\varnothing \in \{\varnothing\}$ 且 $\varnothing \sub \{\varnothing\}$.
递归方式定义集合:
$$
G=\{x \mid x=1 \vee (\exists y)(y\in G \wedge x= \{y\})\}
$$
$$
1 \in G\Rightarrow \{1\}\in G\Rightarrow \{\{1\}\}\in G\Rightarrow \cdots
$$
### 集合之间的关系
集合相等:$A=B \Leftrightarrow (\forall x)(x\in A\leftrightarrow x\in B)$.
集合包含:$A\subseteq B \Leftrightarrow (\forall x)(x\in A\to x\in B)$
集合真包含 $A\sub B \Leftrightarrow (A\subseteq B \wedge \neg (A=B))$.
证明,$A=B\Leftrightarrow (A\subseteq B \wedge B \subseteq A)$.
辨析:
1. $\{a\} \subseteq \{\{a\},b\}$. 错
2. $\{a\}\in \{\{a\},b\}$. 对
3. $\{a\}\subseteq \{a,b,\{a\}\}$. 对
4. $\{a\}\in \{a,b,\{a\}\}$. 对
**空集和全集**
$$
\varnothing = \{x \mid x\not=x\} \quad E=\{x \mid x=x\}
$$
### 集合的运算
定义,对于集合 $A,B$:
- 并集 $A\cup B$ 定义为 $A\cup B=\{x \mid x\in A\vee x\in B\}$.
- 交集 $A\cap B$ 定义为 $A\cap B=\{x\mid x\in A\wedge x\in B\}$.
- 差集(又称 $B$ 对 $A$ 的相对补集)$A-B=\{x\mid x\in A\wedge x\notin B\}$.
- 余集(又称 $A$ 的绝对补集)$-A=E-A=\{x\mid x\notin A\}$. 其中 $E$ 为全集。
- 对称差 $A\oplus B$ 定义为 $(A-B)\cup (B-A)=\{x\mid x\in A\overline{\vee} x\in B\}$.
#### 广义交和广义并
$$
\cup A=\{x\mid (\exists z)(z\in A\wedge x\in z)\}\\
\cap A=\{x\mid (\forall z)(z\in A\to x\in z)\}
$$
规定 $\cup \varnothing = \varnothing$,规定 $\cap \varnothing$ 无意义。
> 因为任意 $z$,$z\in \varnothing$ 必然为 F,则不管什么样的 $x$ 都可以称为 $\cap \varnothing$ 的元素。
用广义交和广义并定义并集和交集:
$$
A\cup B=\cup\{A,B\}\quad A\cap B=\cap \{A,B\}
$$
#### 幂集
$$
P(A)\doteq \{x \mid x\subseteq A\}
$$
幂集一定是一个集合
例如:
$$
P(\varnothing)=\{\varnothing\} \quad P(\{\varnothing\})=\{\varnothing,\{\varnothing\}\}\quad PPP(\varnothing)=\{\varnothing,\{\varnothing\},\{\{\varnothing\}\},\{\varnothing,\{\varnothing\}\}\}
$$
幂集的性质:
$$
P(A)\in P(B)\Rightarrow A\in B
$$
**笛卡尔积**
如何表示两个元素的次序?二元有序对 $\langle x,y\rangle$ 应该具有以下性质:
- $x \not=y \Rightarrow \langle x,y \rangle \not= \langle y,x \rangle$.
- $\langle x,y \rangle=\langle u,v \rangle \Leftrightarrow x=u\wedge y=v$.
有序对 $\langle x,y \rangle $ 定义为 $\{\{x\},\{x,y\}\}$.
> $\{x\}$ 不能写作 $x$.
证明该定义符合有序对的性质:$\langle x,y \rangle=\langle u,v \rangle \Leftrightarrow x=u\wedge y=v$.
左推右显然。右推左:
- 当 $x=y$,则 $\{x\}=\{u\}=\{u,v\}$,因此,$x=y=u=v$.
- 当 $x\not =y$,则只能 $\{x\}=\{u\},\{y\}=\{v\}$.
$n$ 元有序对可以递归定义:
- 当 $n=2$,定义为 $\langle x_1,x_2 \rangle$.
- 当 $n\not=2$,定义为 $\langle x_1,\cdots,x_n \rangle=\langle \langle x_1,\cdots,x_{n-1} \rangle,x_{n-1} \rangle$.
> Q:能不能这样定义:$\{\{x_1\},\{x_1,x_2\},\{x_1,x_2,x_3\}\}$?
>
> 不能分清 $\langle a,b,a \rangle,\langle a,b,b \rangle$
笛卡尔积可以定义为:
$$
A\times B=\{\langle x,y \rangle \mid x\in A\wedge y\in B\}
$$
当 $A=B$ 时可以简写为 $A^2$.
**集合运算的优先权**
- 一元运算符 $(-A,P(A),\cap A,\cup A)$
- 二元运算符($-,\cap,\cup,\oplus,\times$)
- 集合关系符($=,\sube,\sub,\in$)
- 一元联结词($\neg$)
- 二元联结词($\vee,\wedge ,\to , \leftrightarrow$)
- 逻辑关系符($\Leftrightarrow ,\Rightarrow$)
### 集合的图形表示
### 集合运算的关系和证明
#### 集合基本运算的性质
- $$
\begin{array}{c}
A \cup B=B \cup A\\
A \cap B=B \cap A
\end{array}
$$
- $$
\begin{array}{c}
(A \cup B) \cup C=A \cup(B \cup C)\\
(A \cap B) \cap C=A \cap(B \cap C)\
\end{array}
$$
- $$
\begin{array}{c}
A \cup(B \cap C)=(A \cup B) \cap(A \cup C)\\
A \cap(B \cup C)=(A \cap B) \cup(A \cap C)
\end{array}
$$
- $$
\begin{array}{c}
A \cup A=A\\
A \cap A=A
\end{array}
$$
- $$
\begin{array}{c}
A \cup(A \cap B)=A\\
A \cap(A \cup B)=A
\end{array}
$$
- $$
\begin{array}{c}
A-(B \cup C)=(A-B) \cap(A-C)\\
A-(B \cap C)=(A-B) \cup(A-C)\\
-(B \cup C)=-B \cap-C\\
-(B \cap C)=-B \cup-C
\end{array}
$$
- $$
\begin{array}{c}
A \cup \varnothing=A\\
A \cap E=A
\end{array}
$$
- $$
\begin{array}{c}
\quad A \cup E=E\\
A \cap \varnothing=\varnothing
\end{array}
$$
- $$
-(-A)=A
$$
**利用定义的证明**:证明 $A\cup(B\cap C)=(A\cup B)\cap (A\cup C)$. 利用 $P=Q \Leftrightarrow (x\in P \Leftrightarrow x\in Q)$.
$$
\begin{aligned}
&x\in (A\cup (B\cap C))\\
\Leftrightarrow &x\in A\vee x\in B\cap C\\
\Leftrightarrow & x\in A\vee (x\in B\wedge x\in C)\\
\Leftrightarrow & (x\in A\vee x\in B)\cap (x\in A\vee x\in C)\\
\Leftrightarrow & x\in (A\cup B) \wedge x\in (A\cup C)\\
\Leftrightarrow & x\in (A\cup B)\cap (A\cup C)
\end{aligned}
$$
证明 $A\cap (A\cup B)=A$.
$$
A\cap (A\cup B)=(A\cup \varnothing) \cap (A\cup B)=A\cup(\varnothing \cap B)=A\cup\varnothing=A
$$
**利用性质的证明**:
$$
\begin{aligned}
A\cap (B-C)&= A\cap (B\cap -C)\\
&= (A\cap B)\cap -C\\
&=(A\cap B)-C
\end{aligned}
$$
------
证明:对于任意的集合 $A,B,C$,有:
$$
A\cup B=A\cup C,A\cap B=A\cap C \Rightarrow B=C
$$
因为:
$$
B=B\cap (A\cup B)=B\cap (A\cup C)=(B\cap A)\cup (B\cap C)\\=(A\cap C)\cup (B\cap C)=(A\cap B)\cup C=(A\cap C)\cup C=C
$$
--------
**差集的性质**
- $A-B=A-(A\cap B)$.
- $A-B=A\cap -B$. (可以消去 $-$ 符号)
- $A\cup(B-A)=A\cup B$.
- $A\cap (B-C)=(A\cap B)-C$.
----
**对称差的性质**
- 交换律 $A\oplus B=B\oplus A$.
- 结合律 $(A\oplus B)\oplus C=A\oplus(B\oplus C)$.
- 分配律 $A\cap (B\oplus C)=(A\cap B)\oplus (A\cap C)$.
- 同一律 $A\oplus \varnothing =A$.
- 零律 $A\oplus A=\varnothing$.
证明 $A\cap (B\oplus C)=(A\cap B)\oplus (A\cap C)$.
对于任意的 $A,B,C$,给出 $(A-B)\oplus (A-C)=\varnothing$ 的充要条件。
> 即 $A-B=A-C$.
-----
**包含关系的性质**
1. $A\sube B\Rightarrow (A\cup C)\sube (B\cup C)$. 类比:$A\to B\Rightarrow (A\vee C)\to (B\vee C)$.
2. $A\sube B\Rightarrow (A\cap C)\sube (B\cap C)$.
3. $(A\sube B)\wedge (C\sube D)\Rightarrow (A\cup C)\sube (B\cup D)$.
4. $(A\sube B)\wedge (C\sube D)\Rightarrow (A\cap C)\sube (B\cap D)$.
5. $(A\sube B)\wedge (C\sube D)\Rightarrow (A-D)\sube (B-C)$.
6. $C\sube D\Rightarrow (A-D)\sube (A-C)$.
-----------
#### 幂集合的性质
先复习幂集合的定义:
$$
P(A)\doteq \{x \mid x\subseteq A\}
$$
满足性质:
- $x\in P(A)\Rightarrow x\sube A$.
- $A\in P(A)$.
1. $A\sube B\Leftrightarrow P(A)\sube P(B)$. 证明:
1. $x\in P(A)\Leftrightarrow x\sube A(前提 A\sube B)\Rightarrow x\sube B\Leftrightarrow x\in P(B)$.
2. $x\in A\Leftrightarrow \{x\}\sube A \Leftrightarrow \{x\}\in P(A)(前提 P(A)\sube P(B))\Rightarrow \{x\}\in P(B)\Leftrightarrow x\in B$.
2. $A=B\Leftrightarrow P(A)=P(B)$. 利用上面的结论:
$$
\begin{aligned}
A=B&\Leftrightarrow A\sube B \wedge B\sube A\\
&\Leftrightarrow P(A)\sube P(B)\wedge P(B)\sube P(A)\\
&\Leftrightarrow P(A)=P(B)
\end{aligned}
$$
3. $P(A)\in P(B)\Rightarrow A\in B$.
$$
\begin{aligned}
P(A)\in P(B)&\Rightarrow P(A)\sube B\\
&\Rightarrow (P(A)\sube B)\wedge (A\in P(A))\\
&\Rightarrow A\in B
\end{aligned}
$$
反过来不成立,例如 $A=\{\varnothing\},B=\{\{\varnothing\}\}$. 但 $P(A)=\{\varnothing,\{\varnothing\}\}$,$P(B)=\{\varnothing,\{\{\varnothing\}\}\}$.
4. $P(A)\cap P(B)=P(A\cap B)$.
先证明,若 $x\in (P(A)\cap P(B))$,等价于 $x\in P(A)$ 且 $x\in P(B)$,等价于 $x\sube A$ 且 $x\sube B$. 等价于 $x\sube (A\cap B)$. 等价于 $x\in P(A\cap B)$.
> 其中一步的证明: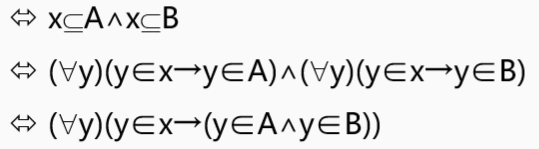 5. $P(A)\cup P(B)\sube P(A\cup B)$.
因为 $x\sube A\vee x\sube B\Rightarrow x\sube A\cup B$. 但是 $x\sube A\cup B\not \Rightarrow x\sube A\vee x\sube B$.
6. $P(A-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
若 $x\in P(A-B)$,**当 $\boldsymbol x$ 不是空集**,则 $x\sube A-B$,可推出 $x\sube A\wedge x\not \sube B$.
因此,$x\in P(A)\wedge x\notin P(B)$. 也就是 $x\in (P(A)-P(B))$. $P(A-B)\sube (P(A)-P(B))\sube (P(A)-P(B))\cup \{\varnothing\}$
**当 $\boldsymbol{x=\varnothing}$**,则显然成立。
> 还可以?首先,$P(-B)=(-P(B))\cup \{\varnothing\}$
>
> $P(A\cap -B)=P(A)\cap P(-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
#### 传递集合
如果集合的集合 $A$ 的任一元素的元素都是 $A$ 的元素,就称 $A$ 为传递集合,这个定义也可以写成:
$$
(\forall x)(\forall y)((x\in y \wedge y\in A)\to x\in A)
$$
等价于:
$$
(\forall y)(y 是集合\wedge y\in A\to y\sube A)
$$
例如,$B=\{\{\varnothing\},\{\varnothing,\{\varnothing\}\}\}$ 不是传递集合。
-----
定理:对集合的集合 $A$,$A$ 是传递集合 $\Leftrightarrow A\sube P(A)$.
先设 $A$ 是传递集合,则对任意的 $y\in A$,若 $y=\varnothing$ 则 $y\in P(A)$. 若 $y\not=\varnothing$,则对于 $(\forall x) (x\in y)$,有 $x\in A$(因为传递集合的性质),则有 $y\sube A$($y$ 中每个元素都是 $A$ 的元素),因此 $y\in P(A)$.
上面我们说明了当 $A$ 是传递集合时,$y\in A\to y\in P(A)$,也就是 $A\sube P(A)$.
再设 $A\sube P(A)$,则对于 $\forall x,\forall y$ 有:
$$
x\in y\wedge y\in A\overset{A\sube P(A)}\Leftrightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A
$$
因此,当 $A\sube P(A)$,$A$ 是传递集合。
---
对集合的集合 $A$,
$$
A 是传递集合 \Leftrightarrow P(A) 是传递集合
$$
先设 $A$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A\Rightarrow x\sube A\Leftrightarrow x\in P(A)
$$
再设 $P(A)$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in A\Leftrightarrow x\in y\wedge \{y\}\sube A\Leftrightarrow x\in y\wedge \{y\}\in P(A)\wedge {\color{gray}{y\in \{y\}}}\\\Rightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y\wedge y\sube A\Rightarrow x\in A
$$
#### 广义并和广义交的性质
对集合的集合 $A,B$,有:
1. $A\sube B\Rightarrow \cup A\sube \cup B$.
2. $A\sube B\Rightarrow \cap B\sube \cap A$,其中 $A,B$ 非空。
证明:利用广义交和广义并的定义。
3. $\cup(A\cup B)=(\cup A)\cup (\cup B)$.
4. $\cap (A\cup B)=(\cap A)\cap (\cap B)$.
证明第一个:
对于 $\forall x$,有:
$$
\begin{aligned}
x\in \cup (A\cup B)&\Leftrightarrow (\exists y)(x\in y \wedge y\in A\cup B)\\
&\Leftrightarrow(\exists y)(x\in y \wedge (y\in A\vee y\in B))\\
&\Leftrightarrow (\exists y)(x\in y\wedge y\in A)\vee (\exists y)(x\in y \wedge y\in B)\\
&\Leftrightarrow x\in \cup A\vee x\in \cup B\Leftrightarrow x\in ((\cup A)\cup (\cup B))
\end{aligned}
$$
5. $\cup (P(A))=A$.
对于 $\forall x$,有:
$$
x\in\cup (P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\in P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\sube A)\Leftrightarrow x\in A
$$
说明了,广义并是幂集的“逆运算”但是 $P(\cup A)\not=A$,只有 $A\sube P(\cup A)$.
6. 若 $A$ 是传递集合,则 $\cup A$ 是传递集合。
> 我们证明 $\cup A$ 是传递集合,其中运用 $A$ 是传递集合的条件。
对于任意 $x$,有:
$$
x\in y\wedge y\in \cup A\overset{因为广义并的定义}\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\\overset{因为A是传递集合}\Rightarrow x\in y \wedge y\in A\Leftrightarrow x\in \cup A
$$
7. 若集合 $A$ 的元素都是传递集合,则 $\cup A$ 是传递集合。
$$
x\in y\wedge y\in \cup A\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\
\Rightarrow (\exists z)(x\in y\wedge y\in z(z 是传递集合)\wedge z\in A)\\
\Rightarrow (\exists z)(x\in z\wedge z\in A)\Rightarrow x\in \cup A
$$
8. 若非空集合 $A$ 是传递集合,则 $\cap A$ 是传递集合,且 $\cap A=\varnothing$.
> 需要使用正则公理。这里暂时不证明
9. 若非空集合 $A$ 的元素都是传递集合,则 $\cap A$ 是传递集合。
$$
\begin{aligned}
x\in y\wedge y\in \cap A&\Leftrightarrow x\in y \wedge (\forall z)(z\in A \to y\in z)\\
&\Rightarrow (\forall z)(x\in y \wedge (z\notin A \vee y\in z))\\
&\Rightarrow (\forall z)((x\in y\wedge z\notin A)\vee (x\in y \wedge y\in z))\\
&\overset{因为 z\in A,是传递集合}\Rightarrow (\forall z)(\neg ((x\not\in y)\vee z\in A)\vee (x\in z))\\
&\Rightarrow(\forall z)(((x\notin y)\vee z\in A)\to (x\in z))\\
&\overset{因为 y 任意}\Rightarrow (\forall z)(z\in A\to x\in z)\\
&\Leftrightarrow x\in \cap A
\end{aligned}
$$
#### 笛卡尔积的性质
> 笛卡尔积可以定义为:
> $$
> A\times B=\{\langle x,y \rangle \mid {\color{red}x\in A\wedge y\in B}\}
> $$
> 有序对 $\langle x,y \rangle $ 定义为 $\{\{x\},\{x,y\}\}$.
1. $A\times \varnothing=\varnothing \times B=\varnothing$.
2. 若 $A\not=\varnothing$ 且 $B\not=\varnothing$ 且 $A\not=B$,则 $A\times B\not =B\times A$.
> 注意条件,少一个都不能满足。
3. $A\times (B\times C)\not =(A\times B)\times C$.
> 因为 $\langle x,\langle y,z \rangle \rangle\not=\langle \langle x,y \rangle,z \rangle$.
4. $\langle x,y \rangle \in A\times B \Leftrightarrow x\in A\wedge y\in B$.
5. 若 $A$ 是集合,$x\in A,y\in A$,则 $\langle x,y \rangle\in PP(A)$.($PP(A)\doteq P(P(A))$)
- $x\in A\Leftrightarrow \{x\}\in P(A)$.
- $x\in A\wedge y\in A\Leftrightarrow \{x,y\}\in P(A)$.
由以上两式可以得到:
$$
x\in A\wedge y\in A\Leftrightarrow \{\{x\},\{x,y\}\}\sube P(A)\Leftrightarrow \langle x,y \rangle \sube P(A)\Leftrightarrow \langle x,y \rangle \in PP(A)
$$
6. 证明 $A\times (B\cup C)=(A\times B)\cup (A\times C)$.
利用结论 4. 我们有:
$$
\begin{aligned}
&\langle x,y \rangle \in A\times (B\cup C)\Leftrightarrow x\in A\wedge y\in B\cup C\\
&\Leftrightarrow x\in A\wedge (y\in B\vee y\in C)\\
&\Leftrightarrow (x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\\
&\Leftrightarrow \langle x,y \rangle\in (A\times B)\vee \langle x,y \rangle\in (A\times C)\\
&\Leftrightarrow \langle x,y \rangle \in (A\times B)\cup (A\times C)
\end{aligned}
$$
7. 对于任意集合 $A,B,C$,若 $C\not=\varnothing$,则:
$$
(A\sube B)\Leftrightarrow (A\times C\sube B\times C)\Leftrightarrow (C\times A\sube C\times B)
$$
利用结论 4. 其实就是对应属于。
8. 对于任意非空集合 $A,B,C,D$,有:
$$
(A\times B\sube C\times D)\Leftrightarrow (A\sube C\wedge B\sube D)
$$
先设 $A\times B \sube C\times D$,对于任意的 $x\in A$,存在 $y\in B$,则:
$$
\langle x,y \rangle \in A\times B \Rightarrow \langle x,y \rangle \in C\times D\Leftrightarrow x\in C\wedge y\in D\Rightarrow x\in C
$$
所以 $x\in A\to x\in C$,$A\sube C$,类似地 $B\sube D$.
再设 $A\sube C\wedge B\sube D$,则:
$$
\langle x,y \rangle \in A\times B\Rightarrow x\in A\wedge y\in B\Rightarrow x\in C\wedge y\in D \Rightarrow \langle x,y \rangle \in C\times D
$$
也就证明了 $A\times B\sube C\times D$.
### 集合的基数
集合的基数就是集合中元素的个数。
**有限集合的基数**
如果存在 $n\in \N$,使得集合 $A$ 与集合 $\{x\mid x\in \N \wedge x 自然数集的大小和自然数集的幂集一样大吗?
**基本运算的基数**
1. $|A_1\cup A_2|\le |A_1|+|A_2|$.
2. $|A_1\cap A_2|\le \min (|A_1|,|A_2|)$.
3. $|A_1-A_2|\ge |A_1|-|A_2|$.
4. $|A_1\oplus A_2|=|A_1|+|A_2|-2|A_1\cap A_2|$.
5. $|A\times B|=|A|\times |B|$.
6. $|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|$.
证明:将 $|A_1|$ 拆分为 $|A_1\cap -A_2|$ 和 $|A_1\cap A_2|$……
**容斥原理**
若 $n\in \N$ 且 $n>1$,$A_1,A_2,\cdots,A_n$ 是有限集合,则:
$$
\begin{aligned}
|A_1\cup A_2\cup \cdots\cup A_n|=&\sum_{i} |A_i|-\sum_{i 为什么规定 $\cap \varnothing $ 不存在。
**正则公理和奇异集合** 首先定义极小元:对于任意集合 $A,B$,当 $A\in B$ 且 $A\cap B=\varnothing$,则称 $A$ 是 $B$ 的一个极小元。正则公理是说一个集合必然存在极小元。
证明:对于任意集合 $A$,$A\notin A$。假设 $A\in A$,构造 $\{A\}$,则 $A\in \{A\}$,且 $\{A\}$ 存在极小元,只能是 $A$,则 $A\cap \{A\}=\varnothing$,但是 $A\in A\Rightarrow A\sube \{A\}\Rightarrow A\cap \{A\}=A$,矛盾。
证明:对于任意的集合 $A_1,A_2$ 有:
$$
\neg(A_1\in A_2\wedge A_2\in A_1)
$$
假设不成立,构造集合 $B=\{A_1,A_2\}$,则 $B$ 存在极小元,
- 假设是 $A_1$,则 $A_1 \cap \{A_1,A_2\}=\varnothing$,但是 $A_1\in A_2 \Rightarrow A_1 \sube \{A_1,A_2\}$,矛盾;
- 假设是 $A_2$,同理矛盾。
证明:对于任意的非空的传递集合 $A$,有 $\varnothing \in A$.
证明:定义奇异集合 $A$,满足 $A_i\in A$,$i=0,1,\cdots$,而且:
$$
\cdots \in A_{n+1}\in A_n\in \cdots \in A_2\in A_1\in A_0
$$
根据正则公理,奇异集合不存在,可以取 $B=\{A_0,A_1,\cdots,A_{n+1}\}$,则假设 $B$ 中有极小元 $A_i$,有:
$$
A_i \in B\wedge A_i \cap B=\varnothing
$$
而 $A_{i+1}\in A_i$,这会使得:
$$
A_{i+1}\in B \Rightarrow A_i\cap B\not=\varnothing
$$
因此矛盾。
**无穷公理和自然数集合**
对于任意集合 $A$,可以定义集合 $A^+=A\cup \{A\}$,把 $A^+$ 称为 $A$ 的后继。
定义自然数:
$$
0=\varnothing,1=0^+=0\cup \{0\}={0},2=1^+=1\cup \{1\}=\{0,1\},\cdots
$$
也就是对于 $n+1$,定义:
$$
n+1=n^+=\{0,1,\cdots,n\}
$$
对于任意自然数 $n,m$,有:
$$
mm\\
m\le n \Leftrightarrow m\sube n \Leftrightarrow n\ge m
$$
集合的三歧性:对于 $A$ 的元素 $A_1,A_2$:$A_1\in A_2,A_1=A_2,A_2\in A_1$ 中恰好成立一个。
自然数的三歧性:即 $mn$ 中恰好成立一个。
5. $P(A)\cup P(B)\sube P(A\cup B)$.
因为 $x\sube A\vee x\sube B\Rightarrow x\sube A\cup B$. 但是 $x\sube A\cup B\not \Rightarrow x\sube A\vee x\sube B$.
6. $P(A-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
若 $x\in P(A-B)$,**当 $\boldsymbol x$ 不是空集**,则 $x\sube A-B$,可推出 $x\sube A\wedge x\not \sube B$.
因此,$x\in P(A)\wedge x\notin P(B)$. 也就是 $x\in (P(A)-P(B))$. $P(A-B)\sube (P(A)-P(B))\sube (P(A)-P(B))\cup \{\varnothing\}$
**当 $\boldsymbol{x=\varnothing}$**,则显然成立。
> 还可以?首先,$P(-B)=(-P(B))\cup \{\varnothing\}$
>
> $P(A\cap -B)=P(A)\cap P(-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
#### 传递集合
如果集合的集合 $A$ 的任一元素的元素都是 $A$ 的元素,就称 $A$ 为传递集合,这个定义也可以写成:
$$
(\forall x)(\forall y)((x\in y \wedge y\in A)\to x\in A)
$$
等价于:
$$
(\forall y)(y 是集合\wedge y\in A\to y\sube A)
$$
例如,$B=\{\{\varnothing\},\{\varnothing,\{\varnothing\}\}\}$ 不是传递集合。
-----
定理:对集合的集合 $A$,$A$ 是传递集合 $\Leftrightarrow A\sube P(A)$.
先设 $A$ 是传递集合,则对任意的 $y\in A$,若 $y=\varnothing$ 则 $y\in P(A)$. 若 $y\not=\varnothing$,则对于 $(\forall x) (x\in y)$,有 $x\in A$(因为传递集合的性质),则有 $y\sube A$($y$ 中每个元素都是 $A$ 的元素),因此 $y\in P(A)$.
上面我们说明了当 $A$ 是传递集合时,$y\in A\to y\in P(A)$,也就是 $A\sube P(A)$.
再设 $A\sube P(A)$,则对于 $\forall x,\forall y$ 有:
$$
x\in y\wedge y\in A\overset{A\sube P(A)}\Leftrightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A
$$
因此,当 $A\sube P(A)$,$A$ 是传递集合。
---
对集合的集合 $A$,
$$
A 是传递集合 \Leftrightarrow P(A) 是传递集合
$$
先设 $A$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A\Rightarrow x\sube A\Leftrightarrow x\in P(A)
$$
再设 $P(A)$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in A\Leftrightarrow x\in y\wedge \{y\}\sube A\Leftrightarrow x\in y\wedge \{y\}\in P(A)\wedge {\color{gray}{y\in \{y\}}}\\\Rightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y\wedge y\sube A\Rightarrow x\in A
$$
#### 广义并和广义交的性质
对集合的集合 $A,B$,有:
1. $A\sube B\Rightarrow \cup A\sube \cup B$.
2. $A\sube B\Rightarrow \cap B\sube \cap A$,其中 $A,B$ 非空。
证明:利用广义交和广义并的定义。
3. $\cup(A\cup B)=(\cup A)\cup (\cup B)$.
4. $\cap (A\cup B)=(\cap A)\cap (\cap B)$.
证明第一个:
对于 $\forall x$,有:
$$
\begin{aligned}
x\in \cup (A\cup B)&\Leftrightarrow (\exists y)(x\in y \wedge y\in A\cup B)\\
&\Leftrightarrow(\exists y)(x\in y \wedge (y\in A\vee y\in B))\\
&\Leftrightarrow (\exists y)(x\in y\wedge y\in A)\vee (\exists y)(x\in y \wedge y\in B)\\
&\Leftrightarrow x\in \cup A\vee x\in \cup B\Leftrightarrow x\in ((\cup A)\cup (\cup B))
\end{aligned}
$$
5. $\cup (P(A))=A$.
对于 $\forall x$,有:
$$
x\in\cup (P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\in P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\sube A)\Leftrightarrow x\in A
$$
说明了,广义并是幂集的“逆运算”但是 $P(\cup A)\not=A$,只有 $A\sube P(\cup A)$.
6. 若 $A$ 是传递集合,则 $\cup A$ 是传递集合。
> 我们证明 $\cup A$ 是传递集合,其中运用 $A$ 是传递集合的条件。
对于任意 $x$,有:
$$
x\in y\wedge y\in \cup A\overset{因为广义并的定义}\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\\overset{因为A是传递集合}\Rightarrow x\in y \wedge y\in A\Leftrightarrow x\in \cup A
$$
7. 若集合 $A$ 的元素都是传递集合,则 $\cup A$ 是传递集合。
$$
x\in y\wedge y\in \cup A\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\
\Rightarrow (\exists z)(x\in y\wedge y\in z(z 是传递集合)\wedge z\in A)\\
\Rightarrow (\exists z)(x\in z\wedge z\in A)\Rightarrow x\in \cup A
$$
8. 若非空集合 $A$ 是传递集合,则 $\cap A$ 是传递集合,且 $\cap A=\varnothing$.
> 需要使用正则公理。这里暂时不证明
9. 若非空集合 $A$ 的元素都是传递集合,则 $\cap A$ 是传递集合。
$$
\begin{aligned}
x\in y\wedge y\in \cap A&\Leftrightarrow x\in y \wedge (\forall z)(z\in A \to y\in z)\\
&\Rightarrow (\forall z)(x\in y \wedge (z\notin A \vee y\in z))\\
&\Rightarrow (\forall z)((x\in y\wedge z\notin A)\vee (x\in y \wedge y\in z))\\
&\overset{因为 z\in A,是传递集合}\Rightarrow (\forall z)(\neg ((x\not\in y)\vee z\in A)\vee (x\in z))\\
&\Rightarrow(\forall z)(((x\notin y)\vee z\in A)\to (x\in z))\\
&\overset{因为 y 任意}\Rightarrow (\forall z)(z\in A\to x\in z)\\
&\Leftrightarrow x\in \cap A
\end{aligned}
$$
#### 笛卡尔积的性质
> 笛卡尔积可以定义为:
> $$
> A\times B=\{\langle x,y \rangle \mid {\color{red}x\in A\wedge y\in B}\}
> $$
> 有序对 $\langle x,y \rangle $ 定义为 $\{\{x\},\{x,y\}\}$.
1. $A\times \varnothing=\varnothing \times B=\varnothing$.
2. 若 $A\not=\varnothing$ 且 $B\not=\varnothing$ 且 $A\not=B$,则 $A\times B\not =B\times A$.
> 注意条件,少一个都不能满足。
3. $A\times (B\times C)\not =(A\times B)\times C$.
> 因为 $\langle x,\langle y,z \rangle \rangle\not=\langle \langle x,y \rangle,z \rangle$.
4. $\langle x,y \rangle \in A\times B \Leftrightarrow x\in A\wedge y\in B$.
5. 若 $A$ 是集合,$x\in A,y\in A$,则 $\langle x,y \rangle\in PP(A)$.($PP(A)\doteq P(P(A))$)
- $x\in A\Leftrightarrow \{x\}\in P(A)$.
- $x\in A\wedge y\in A\Leftrightarrow \{x,y\}\in P(A)$.
由以上两式可以得到:
$$
x\in A\wedge y\in A\Leftrightarrow \{\{x\},\{x,y\}\}\sube P(A)\Leftrightarrow \langle x,y \rangle \sube P(A)\Leftrightarrow \langle x,y \rangle \in PP(A)
$$
6. 证明 $A\times (B\cup C)=(A\times B)\cup (A\times C)$.
利用结论 4. 我们有:
$$
\begin{aligned}
&\langle x,y \rangle \in A\times (B\cup C)\Leftrightarrow x\in A\wedge y\in B\cup C\\
&\Leftrightarrow x\in A\wedge (y\in B\vee y\in C)\\
&\Leftrightarrow (x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\\
&\Leftrightarrow \langle x,y \rangle\in (A\times B)\vee \langle x,y \rangle\in (A\times C)\\
&\Leftrightarrow \langle x,y \rangle \in (A\times B)\cup (A\times C)
\end{aligned}
$$
7. 对于任意集合 $A,B,C$,若 $C\not=\varnothing$,则:
$$
(A\sube B)\Leftrightarrow (A\times C\sube B\times C)\Leftrightarrow (C\times A\sube C\times B)
$$
利用结论 4. 其实就是对应属于。
8. 对于任意非空集合 $A,B,C,D$,有:
$$
(A\times B\sube C\times D)\Leftrightarrow (A\sube C\wedge B\sube D)
$$
先设 $A\times B \sube C\times D$,对于任意的 $x\in A$,存在 $y\in B$,则:
$$
\langle x,y \rangle \in A\times B \Rightarrow \langle x,y \rangle \in C\times D\Leftrightarrow x\in C\wedge y\in D\Rightarrow x\in C
$$
所以 $x\in A\to x\in C$,$A\sube C$,类似地 $B\sube D$.
再设 $A\sube C\wedge B\sube D$,则:
$$
\langle x,y \rangle \in A\times B\Rightarrow x\in A\wedge y\in B\Rightarrow x\in C\wedge y\in D \Rightarrow \langle x,y \rangle \in C\times D
$$
也就证明了 $A\times B\sube C\times D$.
### 集合的基数
集合的基数就是集合中元素的个数。
**有限集合的基数**
如果存在 $n\in \N$,使得集合 $A$ 与集合 $\{x\mid x\in \N \wedge x 自然数集的大小和自然数集的幂集一样大吗?
**基本运算的基数**
1. $|A_1\cup A_2|\le |A_1|+|A_2|$.
2. $|A_1\cap A_2|\le \min (|A_1|,|A_2|)$.
3. $|A_1-A_2|\ge |A_1|-|A_2|$.
4. $|A_1\oplus A_2|=|A_1|+|A_2|-2|A_1\cap A_2|$.
5. $|A\times B|=|A|\times |B|$.
6. $|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|$.
证明:将 $|A_1|$ 拆分为 $|A_1\cap -A_2|$ 和 $|A_1\cap A_2|$……
**容斥原理**
若 $n\in \N$ 且 $n>1$,$A_1,A_2,\cdots,A_n$ 是有限集合,则:
$$
\begin{aligned}
|A_1\cup A_2\cup \cdots\cup A_n|=&\sum_{i} |A_i|-\sum_{i 为什么规定 $\cap \varnothing $ 不存在。
**正则公理和奇异集合** 首先定义极小元:对于任意集合 $A,B$,当 $A\in B$ 且 $A\cap B=\varnothing$,则称 $A$ 是 $B$ 的一个极小元。正则公理是说一个集合必然存在极小元。
证明:对于任意集合 $A$,$A\notin A$。假设 $A\in A$,构造 $\{A\}$,则 $A\in \{A\}$,且 $\{A\}$ 存在极小元,只能是 $A$,则 $A\cap \{A\}=\varnothing$,但是 $A\in A\Rightarrow A\sube \{A\}\Rightarrow A\cap \{A\}=A$,矛盾。
证明:对于任意的集合 $A_1,A_2$ 有:
$$
\neg(A_1\in A_2\wedge A_2\in A_1)
$$
假设不成立,构造集合 $B=\{A_1,A_2\}$,则 $B$ 存在极小元,
- 假设是 $A_1$,则 $A_1 \cap \{A_1,A_2\}=\varnothing$,但是 $A_1\in A_2 \Rightarrow A_1 \sube \{A_1,A_2\}$,矛盾;
- 假设是 $A_2$,同理矛盾。
证明:对于任意的非空的传递集合 $A$,有 $\varnothing \in A$.
证明:定义奇异集合 $A$,满足 $A_i\in A$,$i=0,1,\cdots$,而且:
$$
\cdots \in A_{n+1}\in A_n\in \cdots \in A_2\in A_1\in A_0
$$
根据正则公理,奇异集合不存在,可以取 $B=\{A_0,A_1,\cdots,A_{n+1}\}$,则假设 $B$ 中有极小元 $A_i$,有:
$$
A_i \in B\wedge A_i \cap B=\varnothing
$$
而 $A_{i+1}\in A_i$,这会使得:
$$
A_{i+1}\in B \Rightarrow A_i\cap B\not=\varnothing
$$
因此矛盾。
**无穷公理和自然数集合**
对于任意集合 $A$,可以定义集合 $A^+=A\cup \{A\}$,把 $A^+$ 称为 $A$ 的后继。
定义自然数:
$$
0=\varnothing,1=0^+=0\cup \{0\}={0},2=1^+=1\cup \{1\}=\{0,1\},\cdots
$$
也就是对于 $n+1$,定义:
$$
n+1=n^+=\{0,1,\cdots,n\}
$$
对于任意自然数 $n,m$,有:
$$
mm\\
m\le n \Leftrightarrow m\sube n \Leftrightarrow n\ge m
$$
集合的三歧性:对于 $A$ 的元素 $A_1,A_2$:$A_1\in A_2,A_1=A_2,A_2\in A_1$ 中恰好成立一个。
自然数的三歧性:即 $mn$ 中恰好成立一个。
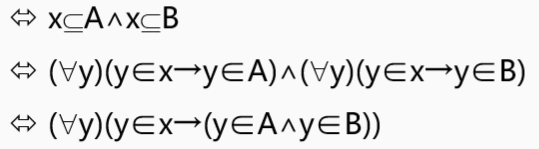 5. $P(A)\cup P(B)\sube P(A\cup B)$.
因为 $x\sube A\vee x\sube B\Rightarrow x\sube A\cup B$. 但是 $x\sube A\cup B\not \Rightarrow x\sube A\vee x\sube B$.
6. $P(A-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
若 $x\in P(A-B)$,**当 $\boldsymbol x$ 不是空集**,则 $x\sube A-B$,可推出 $x\sube A\wedge x\not \sube B$.
因此,$x\in P(A)\wedge x\notin P(B)$. 也就是 $x\in (P(A)-P(B))$. $P(A-B)\sube (P(A)-P(B))\sube (P(A)-P(B))\cup \{\varnothing\}$
**当 $\boldsymbol{x=\varnothing}$**,则显然成立。
> 还可以?首先,$P(-B)=(-P(B))\cup \{\varnothing\}$
>
> $P(A\cap -B)=P(A)\cap P(-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
#### 传递集合
如果集合的集合 $A$ 的任一元素的元素都是 $A$ 的元素,就称 $A$ 为传递集合,这个定义也可以写成:
$$
(\forall x)(\forall y)((x\in y \wedge y\in A)\to x\in A)
$$
等价于:
$$
(\forall y)(y 是集合\wedge y\in A\to y\sube A)
$$
例如,$B=\{\{\varnothing\},\{\varnothing,\{\varnothing\}\}\}$ 不是传递集合。
-----
定理:对集合的集合 $A$,$A$ 是传递集合 $\Leftrightarrow A\sube P(A)$.
先设 $A$ 是传递集合,则对任意的 $y\in A$,若 $y=\varnothing$ 则 $y\in P(A)$. 若 $y\not=\varnothing$,则对于 $(\forall x) (x\in y)$,有 $x\in A$(因为传递集合的性质),则有 $y\sube A$($y$ 中每个元素都是 $A$ 的元素),因此 $y\in P(A)$.
上面我们说明了当 $A$ 是传递集合时,$y\in A\to y\in P(A)$,也就是 $A\sube P(A)$.
再设 $A\sube P(A)$,则对于 $\forall x,\forall y$ 有:
$$
x\in y\wedge y\in A\overset{A\sube P(A)}\Leftrightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A
$$
因此,当 $A\sube P(A)$,$A$ 是传递集合。
---
对集合的集合 $A$,
$$
A 是传递集合 \Leftrightarrow P(A) 是传递集合
$$
先设 $A$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A\Rightarrow x\sube A\Leftrightarrow x\in P(A)
$$
再设 $P(A)$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in A\Leftrightarrow x\in y\wedge \{y\}\sube A\Leftrightarrow x\in y\wedge \{y\}\in P(A)\wedge {\color{gray}{y\in \{y\}}}\\\Rightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y\wedge y\sube A\Rightarrow x\in A
$$
#### 广义并和广义交的性质
对集合的集合 $A,B$,有:
1. $A\sube B\Rightarrow \cup A\sube \cup B$.
2. $A\sube B\Rightarrow \cap B\sube \cap A$,其中 $A,B$ 非空。
证明:利用广义交和广义并的定义。
3. $\cup(A\cup B)=(\cup A)\cup (\cup B)$.
4. $\cap (A\cup B)=(\cap A)\cap (\cap B)$.
证明第一个:
对于 $\forall x$,有:
$$
\begin{aligned}
x\in \cup (A\cup B)&\Leftrightarrow (\exists y)(x\in y \wedge y\in A\cup B)\\
&\Leftrightarrow(\exists y)(x\in y \wedge (y\in A\vee y\in B))\\
&\Leftrightarrow (\exists y)(x\in y\wedge y\in A)\vee (\exists y)(x\in y \wedge y\in B)\\
&\Leftrightarrow x\in \cup A\vee x\in \cup B\Leftrightarrow x\in ((\cup A)\cup (\cup B))
\end{aligned}
$$
5. $\cup (P(A))=A$.
对于 $\forall x$,有:
$$
x\in\cup (P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\in P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\sube A)\Leftrightarrow x\in A
$$
说明了,广义并是幂集的“逆运算”但是 $P(\cup A)\not=A$,只有 $A\sube P(\cup A)$.
6. 若 $A$ 是传递集合,则 $\cup A$ 是传递集合。
> 我们证明 $\cup A$ 是传递集合,其中运用 $A$ 是传递集合的条件。
对于任意 $x$,有:
$$
x\in y\wedge y\in \cup A\overset{因为广义并的定义}\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\\overset{因为A是传递集合}\Rightarrow x\in y \wedge y\in A\Leftrightarrow x\in \cup A
$$
7. 若集合 $A$ 的元素都是传递集合,则 $\cup A$ 是传递集合。
$$
x\in y\wedge y\in \cup A\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\
\Rightarrow (\exists z)(x\in y\wedge y\in z(z 是传递集合)\wedge z\in A)\\
\Rightarrow (\exists z)(x\in z\wedge z\in A)\Rightarrow x\in \cup A
$$
8. 若非空集合 $A$ 是传递集合,则 $\cap A$ 是传递集合,且 $\cap A=\varnothing$.
> 需要使用正则公理。这里暂时不证明
9. 若非空集合 $A$ 的元素都是传递集合,则 $\cap A$ 是传递集合。
$$
\begin{aligned}
x\in y\wedge y\in \cap A&\Leftrightarrow x\in y \wedge (\forall z)(z\in A \to y\in z)\\
&\Rightarrow (\forall z)(x\in y \wedge (z\notin A \vee y\in z))\\
&\Rightarrow (\forall z)((x\in y\wedge z\notin A)\vee (x\in y \wedge y\in z))\\
&\overset{因为 z\in A,是传递集合}\Rightarrow (\forall z)(\neg ((x\not\in y)\vee z\in A)\vee (x\in z))\\
&\Rightarrow(\forall z)(((x\notin y)\vee z\in A)\to (x\in z))\\
&\overset{因为 y 任意}\Rightarrow (\forall z)(z\in A\to x\in z)\\
&\Leftrightarrow x\in \cap A
\end{aligned}
$$
#### 笛卡尔积的性质
> 笛卡尔积可以定义为:
> $$
> A\times B=\{\langle x,y \rangle \mid {\color{red}x\in A\wedge y\in B}\}
> $$
> 有序对 $\langle x,y \rangle $ 定义为 $\{\{x\},\{x,y\}\}$.
1. $A\times \varnothing=\varnothing \times B=\varnothing$.
2. 若 $A\not=\varnothing$ 且 $B\not=\varnothing$ 且 $A\not=B$,则 $A\times B\not =B\times A$.
> 注意条件,少一个都不能满足。
3. $A\times (B\times C)\not =(A\times B)\times C$.
> 因为 $\langle x,\langle y,z \rangle \rangle\not=\langle \langle x,y \rangle,z \rangle$.
4. $\langle x,y \rangle \in A\times B \Leftrightarrow x\in A\wedge y\in B$.
5. 若 $A$ 是集合,$x\in A,y\in A$,则 $\langle x,y \rangle\in PP(A)$.($PP(A)\doteq P(P(A))$)
- $x\in A\Leftrightarrow \{x\}\in P(A)$.
- $x\in A\wedge y\in A\Leftrightarrow \{x,y\}\in P(A)$.
由以上两式可以得到:
$$
x\in A\wedge y\in A\Leftrightarrow \{\{x\},\{x,y\}\}\sube P(A)\Leftrightarrow \langle x,y \rangle \sube P(A)\Leftrightarrow \langle x,y \rangle \in PP(A)
$$
6. 证明 $A\times (B\cup C)=(A\times B)\cup (A\times C)$.
利用结论 4. 我们有:
$$
\begin{aligned}
&\langle x,y \rangle \in A\times (B\cup C)\Leftrightarrow x\in A\wedge y\in B\cup C\\
&\Leftrightarrow x\in A\wedge (y\in B\vee y\in C)\\
&\Leftrightarrow (x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\\
&\Leftrightarrow \langle x,y \rangle\in (A\times B)\vee \langle x,y \rangle\in (A\times C)\\
&\Leftrightarrow \langle x,y \rangle \in (A\times B)\cup (A\times C)
\end{aligned}
$$
7. 对于任意集合 $A,B,C$,若 $C\not=\varnothing$,则:
$$
(A\sube B)\Leftrightarrow (A\times C\sube B\times C)\Leftrightarrow (C\times A\sube C\times B)
$$
利用结论 4. 其实就是对应属于。
8. 对于任意非空集合 $A,B,C,D$,有:
$$
(A\times B\sube C\times D)\Leftrightarrow (A\sube C\wedge B\sube D)
$$
先设 $A\times B \sube C\times D$,对于任意的 $x\in A$,存在 $y\in B$,则:
$$
\langle x,y \rangle \in A\times B \Rightarrow \langle x,y \rangle \in C\times D\Leftrightarrow x\in C\wedge y\in D\Rightarrow x\in C
$$
所以 $x\in A\to x\in C$,$A\sube C$,类似地 $B\sube D$.
再设 $A\sube C\wedge B\sube D$,则:
$$
\langle x,y \rangle \in A\times B\Rightarrow x\in A\wedge y\in B\Rightarrow x\in C\wedge y\in D \Rightarrow \langle x,y \rangle \in C\times D
$$
也就证明了 $A\times B\sube C\times D$.
### 集合的基数
集合的基数就是集合中元素的个数。
**有限集合的基数**
如果存在 $n\in \N$,使得集合 $A$ 与集合 $\{x\mid x\in \N \wedge x
5. $P(A)\cup P(B)\sube P(A\cup B)$.
因为 $x\sube A\vee x\sube B\Rightarrow x\sube A\cup B$. 但是 $x\sube A\cup B\not \Rightarrow x\sube A\vee x\sube B$.
6. $P(A-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
若 $x\in P(A-B)$,**当 $\boldsymbol x$ 不是空集**,则 $x\sube A-B$,可推出 $x\sube A\wedge x\not \sube B$.
因此,$x\in P(A)\wedge x\notin P(B)$. 也就是 $x\in (P(A)-P(B))$. $P(A-B)\sube (P(A)-P(B))\sube (P(A)-P(B))\cup \{\varnothing\}$
**当 $\boldsymbol{x=\varnothing}$**,则显然成立。
> 还可以?首先,$P(-B)=(-P(B))\cup \{\varnothing\}$
>
> $P(A\cap -B)=P(A)\cap P(-B)\sube (P(A)-P(B))\cup \{\varnothing\}$.
#### 传递集合
如果集合的集合 $A$ 的任一元素的元素都是 $A$ 的元素,就称 $A$ 为传递集合,这个定义也可以写成:
$$
(\forall x)(\forall y)((x\in y \wedge y\in A)\to x\in A)
$$
等价于:
$$
(\forall y)(y 是集合\wedge y\in A\to y\sube A)
$$
例如,$B=\{\{\varnothing\},\{\varnothing,\{\varnothing\}\}\}$ 不是传递集合。
-----
定理:对集合的集合 $A$,$A$ 是传递集合 $\Leftrightarrow A\sube P(A)$.
先设 $A$ 是传递集合,则对任意的 $y\in A$,若 $y=\varnothing$ 则 $y\in P(A)$. 若 $y\not=\varnothing$,则对于 $(\forall x) (x\in y)$,有 $x\in A$(因为传递集合的性质),则有 $y\sube A$($y$ 中每个元素都是 $A$ 的元素),因此 $y\in P(A)$.
上面我们说明了当 $A$ 是传递集合时,$y\in A\to y\in P(A)$,也就是 $A\sube P(A)$.
再设 $A\sube P(A)$,则对于 $\forall x,\forall y$ 有:
$$
x\in y\wedge y\in A\overset{A\sube P(A)}\Leftrightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A
$$
因此,当 $A\sube P(A)$,$A$ 是传递集合。
---
对集合的集合 $A$,
$$
A 是传递集合 \Leftrightarrow P(A) 是传递集合
$$
先设 $A$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in P(A)\Leftrightarrow x\in y \wedge y\sube A\Rightarrow x\in A\Rightarrow x\sube A\Leftrightarrow x\in P(A)
$$
再设 $P(A)$ 是传递集合,对于任意的 $x,y$ 有:
$$
x\in y\wedge y\in A\Leftrightarrow x\in y\wedge \{y\}\sube A\Leftrightarrow x\in y\wedge \{y\}\in P(A)\wedge {\color{gray}{y\in \{y\}}}\\\Rightarrow x\in y \wedge y\in P(A)\Leftrightarrow x\in y\wedge y\sube A\Rightarrow x\in A
$$
#### 广义并和广义交的性质
对集合的集合 $A,B$,有:
1. $A\sube B\Rightarrow \cup A\sube \cup B$.
2. $A\sube B\Rightarrow \cap B\sube \cap A$,其中 $A,B$ 非空。
证明:利用广义交和广义并的定义。
3. $\cup(A\cup B)=(\cup A)\cup (\cup B)$.
4. $\cap (A\cup B)=(\cap A)\cap (\cap B)$.
证明第一个:
对于 $\forall x$,有:
$$
\begin{aligned}
x\in \cup (A\cup B)&\Leftrightarrow (\exists y)(x\in y \wedge y\in A\cup B)\\
&\Leftrightarrow(\exists y)(x\in y \wedge (y\in A\vee y\in B))\\
&\Leftrightarrow (\exists y)(x\in y\wedge y\in A)\vee (\exists y)(x\in y \wedge y\in B)\\
&\Leftrightarrow x\in \cup A\vee x\in \cup B\Leftrightarrow x\in ((\cup A)\cup (\cup B))
\end{aligned}
$$
5. $\cup (P(A))=A$.
对于 $\forall x$,有:
$$
x\in\cup (P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\in P(A))\Leftrightarrow (\exists y)(x\in y\wedge y\sube A)\Leftrightarrow x\in A
$$
说明了,广义并是幂集的“逆运算”但是 $P(\cup A)\not=A$,只有 $A\sube P(\cup A)$.
6. 若 $A$ 是传递集合,则 $\cup A$ 是传递集合。
> 我们证明 $\cup A$ 是传递集合,其中运用 $A$ 是传递集合的条件。
对于任意 $x$,有:
$$
x\in y\wedge y\in \cup A\overset{因为广义并的定义}\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\\overset{因为A是传递集合}\Rightarrow x\in y \wedge y\in A\Leftrightarrow x\in \cup A
$$
7. 若集合 $A$ 的元素都是传递集合,则 $\cup A$ 是传递集合。
$$
x\in y\wedge y\in \cup A\Leftrightarrow x\in y \wedge (\exists z)(y\in z\wedge z\in A)\\
\Rightarrow (\exists z)(x\in y\wedge y\in z(z 是传递集合)\wedge z\in A)\\
\Rightarrow (\exists z)(x\in z\wedge z\in A)\Rightarrow x\in \cup A
$$
8. 若非空集合 $A$ 是传递集合,则 $\cap A$ 是传递集合,且 $\cap A=\varnothing$.
> 需要使用正则公理。这里暂时不证明
9. 若非空集合 $A$ 的元素都是传递集合,则 $\cap A$ 是传递集合。
$$
\begin{aligned}
x\in y\wedge y\in \cap A&\Leftrightarrow x\in y \wedge (\forall z)(z\in A \to y\in z)\\
&\Rightarrow (\forall z)(x\in y \wedge (z\notin A \vee y\in z))\\
&\Rightarrow (\forall z)((x\in y\wedge z\notin A)\vee (x\in y \wedge y\in z))\\
&\overset{因为 z\in A,是传递集合}\Rightarrow (\forall z)(\neg ((x\not\in y)\vee z\in A)\vee (x\in z))\\
&\Rightarrow(\forall z)(((x\notin y)\vee z\in A)\to (x\in z))\\
&\overset{因为 y 任意}\Rightarrow (\forall z)(z\in A\to x\in z)\\
&\Leftrightarrow x\in \cap A
\end{aligned}
$$
#### 笛卡尔积的性质
> 笛卡尔积可以定义为:
> $$
> A\times B=\{\langle x,y \rangle \mid {\color{red}x\in A\wedge y\in B}\}
> $$
> 有序对 $\langle x,y \rangle $ 定义为 $\{\{x\},\{x,y\}\}$.
1. $A\times \varnothing=\varnothing \times B=\varnothing$.
2. 若 $A\not=\varnothing$ 且 $B\not=\varnothing$ 且 $A\not=B$,则 $A\times B\not =B\times A$.
> 注意条件,少一个都不能满足。
3. $A\times (B\times C)\not =(A\times B)\times C$.
> 因为 $\langle x,\langle y,z \rangle \rangle\not=\langle \langle x,y \rangle,z \rangle$.
4. $\langle x,y \rangle \in A\times B \Leftrightarrow x\in A\wedge y\in B$.
5. 若 $A$ 是集合,$x\in A,y\in A$,则 $\langle x,y \rangle\in PP(A)$.($PP(A)\doteq P(P(A))$)
- $x\in A\Leftrightarrow \{x\}\in P(A)$.
- $x\in A\wedge y\in A\Leftrightarrow \{x,y\}\in P(A)$.
由以上两式可以得到:
$$
x\in A\wedge y\in A\Leftrightarrow \{\{x\},\{x,y\}\}\sube P(A)\Leftrightarrow \langle x,y \rangle \sube P(A)\Leftrightarrow \langle x,y \rangle \in PP(A)
$$
6. 证明 $A\times (B\cup C)=(A\times B)\cup (A\times C)$.
利用结论 4. 我们有:
$$
\begin{aligned}
&\langle x,y \rangle \in A\times (B\cup C)\Leftrightarrow x\in A\wedge y\in B\cup C\\
&\Leftrightarrow x\in A\wedge (y\in B\vee y\in C)\\
&\Leftrightarrow (x\in A\wedge y\in B)\vee (x\in A\wedge y\in C)\\
&\Leftrightarrow \langle x,y \rangle\in (A\times B)\vee \langle x,y \rangle\in (A\times C)\\
&\Leftrightarrow \langle x,y \rangle \in (A\times B)\cup (A\times C)
\end{aligned}
$$
7. 对于任意集合 $A,B,C$,若 $C\not=\varnothing$,则:
$$
(A\sube B)\Leftrightarrow (A\times C\sube B\times C)\Leftrightarrow (C\times A\sube C\times B)
$$
利用结论 4. 其实就是对应属于。
8. 对于任意非空集合 $A,B,C,D$,有:
$$
(A\times B\sube C\times D)\Leftrightarrow (A\sube C\wedge B\sube D)
$$
先设 $A\times B \sube C\times D$,对于任意的 $x\in A$,存在 $y\in B$,则:
$$
\langle x,y \rangle \in A\times B \Rightarrow \langle x,y \rangle \in C\times D\Leftrightarrow x\in C\wedge y\in D\Rightarrow x\in C
$$
所以 $x\in A\to x\in C$,$A\sube C$,类似地 $B\sube D$.
再设 $A\sube C\wedge B\sube D$,则:
$$
\langle x,y \rangle \in A\times B\Rightarrow x\in A\wedge y\in B\Rightarrow x\in C\wedge y\in D \Rightarrow \langle x,y \rangle \in C\times D
$$
也就证明了 $A\times B\sube C\times D$.
### 集合的基数
集合的基数就是集合中元素的个数。
**有限集合的基数**
如果存在 $n\in \N$,使得集合 $A$ 与集合 $\{x\mid x\in \N \wedge x